色々な関数をsympyで書いて可視化してみた

最近LSTMを学んでいるのですが、ハイパボリックタンジェントやらシグモイドやらReLUやら色々出てきて、

どれがどれか忘れてしまうので、sympyを使って関数を書き可視化してみました。

この記事は追記していく予定です。

ちなみにsinやcosなどをマクローリン展開した記事も書いてます。

seiya-typ.hatenablog.com

まずはライブラリをインポートして各種設定をしておきます。

import numpy as np
import math
import sympy
from sympy.plotting import plot
sympy.init_printing(use_unicode=True)

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

tanh（ハイパボリックタンジェント）

tanhの数式は以下のようになります。

$ f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} $

たとえばLSTMでは、入力と一つ前の出力との和をtanhに通すことで、-1 ~ +1 の範囲に正規化するなどします。

$ h_t = tanh(x_t + h_{t-1}) $

なぜtanhなのかというと、２次微分の減衰がかなりゆっくりとゼロになり勾配消失問題が起きにくいためのようです。

では実装、可視化していきます。

def tanh(x):
  return (sympy.exp(x) - sympy.exp(-x)) / (sympy.exp(x) + sympy.exp(-x))

x = sympy.symbols("x")
formula = tanh(x)
plt.rcParams['figure.figsize'] = 10, 8
ax = sympy.plot(formula, show=False)

ax.show()

xが x < -2.5 では-1、x > +2.5では1に近くなる、といった感じですね。

sigmoid

sigmoid関数は、以下の式で表せます。

$ f(x) = \frac{1}{1+exp(-x)} $

sigmoid関数を通すことで、0 ~ +1 の範囲に正規化することができます。

それでは実装、可視化していきます。

def sigmoid(x):
  return 1 / (1 + sympy.exp(-x))

x = sympy.symbols('x')
formula = sigmoid(x)
plt.rcParams['figure.figsize'] = 10, 8
ax = sympy.plot(formula, (x, -10, 10))

ax.show()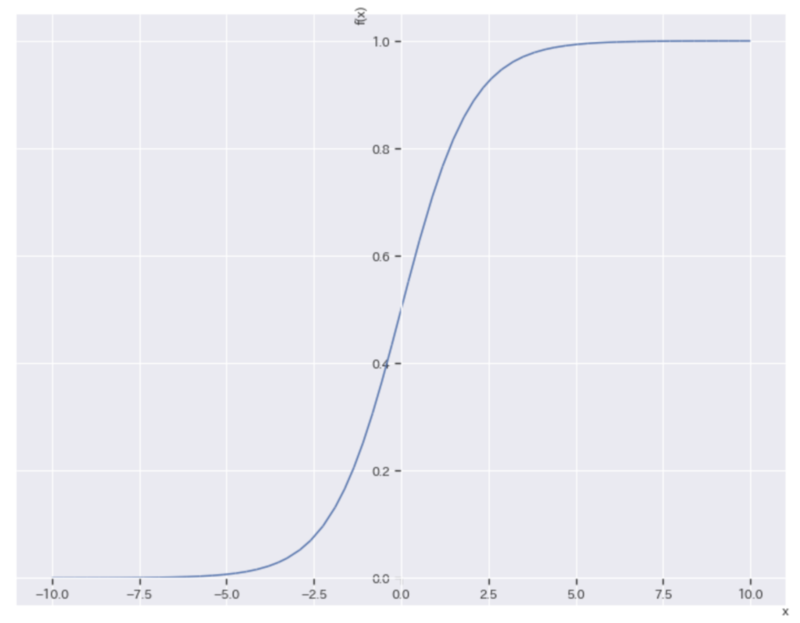

tanhよりも少し緩やかな曲線を描いています。x <-5 では0、x> +5 では1に近くなっています。

Relu

Reluは入力が正のときはそのまま出力して、負の場合は0にするというものです。

def relu(x):
  return sympy.Max(x, 0)

x = sympy.symbols('x')
formula = relu(x)
plt.rcParams['figure.figsize'] = 10, 8
ax = sympy.plot(formula, show=False)

ax.show()

ニューラルネットの活性化関数として紹介されるのをよく見ます。

tanh、sigmoid、ReLUを重ねて比較してみます。

x = sympy.symbols("x")
formula1 = tanh(x)
formula2 = sigmoid(x)
formula3 = relu(x)

plt.rcParams['figure.figsize'] = 10, 8
ax = sympy.plot(formula1, formula2, formula3,
                legend=True, show=False)

ax[0].line_color="blue"
ax[0].label='$tanh(x)$'
ax[1].line_color="orange"
ax[1].label='$sigmoid(x)$'
ax[2].line_color="green"
ax[2].label='$relu(x)$'

ax.ylim = (-1.5, 1.5)

ax.show()